Singapour caracole en tête des classements internationaux en maths. Du coup, sa méthode a été étudiée de près par quantité de chercheurs. Elle est désormais reprise par de nombreux pays soucieux de performance en mathématiques comme Israël, l’Afrique du Sud, l’Arabie Saoudite, l’Allemagne, l’Inde, l’Indonésie, Taïwan… La méthode de mathématiques de Singapour est utilisée par nombre d’écoles indépendantes françaises. Jean-Michel Jamet, un instituteur qui la connaît bien, nous en présente les spécificités et invite ceux qui l’utilisent à mutualiser leurs réflexions et bonnes pratiques sur un site dédié à cet effet : www.singamath.fr.
Le blog de la liberté scolaire : Quelle est l’origine de la méthode de Singapour ? Qui l’a conçue ? Qui l’utilise aujourd’hui dans le monde ? Quelle preuve de son efficacité a-t-on ?
Jean-Michel Jamet : La méthode dite « de Singapour » est le fruit d’un long travail mené par une équipe de didacticiens en mathématiques soutenue par le ministère de Singapour depuis 1980.
La « méthode de Singapour » est une des rares méthodes de mathématiques aujourd’hui à synthétiser en elle-même un ensemble de démarches didactiques validées par la recherche en enseignement efficace. Les élèves utilisant la méthode de Singapour dans son intégralité apparaissent compétents aussi bien dans la maîtrise des concepts mathématiques, en calcul qu’en résolution de problèmes. Ce dernier domaine des mathématiques, révélant souvent des disparités d’expertises chez les élèves fait l’objet d’un travail spécifique dans la méthode.
Ce sont principalement les évaluations internationales TIMMS (évaluations spécialisées dans les domaines des mathématiques et des sciences) de 1995, 1999 et 2003 qui ont révélé chez les élèves utilisant cette méthode des performances excellentes dans de nombreux domaines constituant les mathématiques (calculs sur les fractions, résolution de problèmes, etc.) Depuis 2003, Singapour reste classé parmi les premiers pays à pouvoir dispenser un enseignement de qualité et d’excellence à ses élèves de primaire et collège concernant le champ des mathématiques.
Un exercice incluant des schémas de barres rectangulaires.
Depuis une dizaine d’années, de nombreux pays importent l’édition américaine tels que l’Afrique du Sud, l’Arabie Saoudite, la Jordanie, le Chili, le Panama, l’Allemagne, l’Inde, l’Indonésie, les Philippines et Taïwan.
Sur quels principes repose-t-elle ? En quoi diffère-t-elle des méthodes classiques pratiquées dans les années 1950 ainsi que de celles qui sont actuellement utilisées comme Picbille ?
J.-M. J. : Difficile de résumer quarante années de recherche en quelques lignes ! Pour simplifier, disons que pour l’ensemble des notions travaillées, la méthode suit une progression très rigoureuse basée sur une appropriation graduelle des concepts selon trois étapes : une étape dite « concrète » (présentation concrète d’objets ou manipulation), puis vient une « représentation imagée » (présentée dans le manuel) qui est une occasion de verbaliser les éléments importants du concept travaillé et enfin une présentation « formelle » qu’on pourrait qualifier « d’abstraite ».
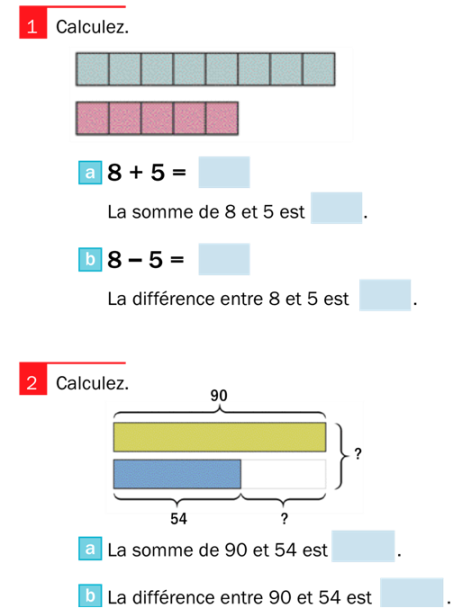
Ensuite, la méthode de Singapour est appelée ailleurs la « méthode par modélisation », celle-ci propose en effet aux enseignants et élèves d’adopter une démarche de résolution des problèmes inhabituelle : il s’agit – à l’aide d’un schéma réalisé avec des barres rectangulaires – de mettre en lumière et d’expliciter ainsi les données en jeu présentées dans un problème. Cette démarche de résolution est spécifique à cette méthode qui a ainsi développé toute une pratique pédagogique très élaborée pour aider les élèves dans ce champ disciplinaire qui pose souvent des difficultés aux élèves… mais aussi aux enseignants !
Par ailleurs, une différence notable avec nos méthodes actuelles est la progression de type « massée » : une même notion est travaillée sur une période d’enseignement continue (trois semaines sur la multiplication, sur la division…). Cette progression très efficace pour les élèves en difficulté qui présentent souvent une faible rétention des informations en mémoire à court et moyen terme requiert un usage régulier des révisions.
Quelles bonnes raisons donneriez-vous aux instituteurs d’aujourd’hui d’utiliser cette méthode ? Cette méthode a-t-elle des défauts ou présente-t-elle des difficultés particulières ?
J.-M.J. : Il s’agit tout d’abord d’une méthode éprouvée. Non seulement par l’expérience de milliers d’enseignants mais aussi par des évaluations standardisées, des recherches dans le domaine de l’enseignement efficace des mathématiques. Ainsi, choisir une méthode qui « a fait ses preuves » est gage de sérénité pour l’enseignant… Ce n’est pas rien !
Ensuite, cette méthode, de par sa progression et les nombreux visuels employés donne le « goût » des mathématiques aux élèves brillants mais aussi à ceux qui peinent… elle est attractive dans le sens pédagogique (les élèves s’impliquent) et aussi affectif (les visuels et les manuels donnent valeur aux mathématiques dans la classe).
Enfin, la progression « massée » de chaque notion la rend aisée à utiliser et permet de diagnostiquer chez les élèves les difficultés fondamentales qui peuvent émerger lors de l’enseignement-apprentissage d’une notion, celle-ci étant travaillée de jour en jour sur une période continue.
Bien sûr, toute méthode possède des défauts… Ceux-ci sont d’ailleurs souvent l’envers des qualités ! Pour la méthode dite « de Singapour », il en est de même… L’usage de graphiques ou de « modèles en barres » dans la résolution de problèmes peut aussi être interprété par l’enseignant ou le parent comme une traduction visuelle « directe », utilisable comme un mode opératoire magique. Il suffirait de dessiner pour comprendre un problème…
La réalité est bien plus complexe et bien plus passionnante également ! Quand on travaille avec des enfants, on travaille avec des « petits d’hommes » qui veulent « comprendre… » Or, aucune compréhension ne peut se passer de langage… Au sens étymologique, « comprendre » c’est « prendre avec soi », or on ne peut comprendre, « prendre avec soi », que si l’on se sent un minimum engagé et investi dans la tâche !
Ainsi, en dehors d’une implication que l’on pourrait qualifier de « cognitive » de la part de l’élève dans la construction, l’élaboration du modèle en barre ou du graphique aidant la résolution de problème, il y a un risque que cette représentation visuelle ne rejoigne pas le niveau de compréhension de l’élève.
Comment impliquer l’élève dans cette construction du sens des données exposées par le problème ?
J.-M.J. : Sur cette question, la littérature en enseignement efficace ne manque pas ! On pourra juste retenir de façon très concrète :
1 – prendre le temps d’accompagner l’élève lors de l’enseignement d’une notion. Car il ne suffit pas d’exposer le plus simplement et clairement possible un concept pour que celui-ci soit compris de l’élève ! Il faut aussi, lors de ce qu’on appelle une « pratique guidée » vérifier immédiatement sa compréhension, ajuster ses propres explications et fournir un entraînement adéquat.
2 – un questionnement très fréquent de l’élève (dans notre cas, portant sur les raisons qui fondent le choix du graphique : pourquoi tel graphique plutôt qu’un autre ? peux-tu justifier ton calcul à l’aide du graphique ? etc.)
3 – inviter les élèves à « penser à voix haute » ! Nombreuses sont les occasions d’expliciter ses procédures, ses façons de faire et dans la méthode de Singapour, les visuels permettent de travailler le langage mathématique et la précision de l’argumentation mathématique depuis le C.P – niveau pour lequel les élèves doivent parfois « inventer » des courtes histoires répondant à une situation mathématique illustrée jusqu’au CM2 où bien évidemment la résolution de problème et sa démarche de résolution tiennent également une place centrale.
Quels conseils pratique donneriez-vous aux enseignants qui souhaitent la mettre en place ?
- mutualisez… ! Les ressources en français sur la méthode de Singapour sont encore trop réduites pour aider les enseignants à percevoir toute la richesse pédagogique, la complexité aussi, et surtout l’efficacité de la méthode dite « de Singapour ». C’est la raison pour laquelle nous avons créé notre site singamath.fr en espérant, petit à petit, en faire un outil précieux répondant à une réelle demande, à un réel besoin de la part des enseignants. Dans ce site, nous essayons de fournir des supports mais aussi une réflexion – légère – sur l’enseignement des mathématiques nourrie par les études en enseignement efficace.
- concertez… vous ! Je ne préconise pas d’adopter cette méthode en fin de scolarité primaire si elle n’a pas fait l’objet d’un travail en amont auprès des élèves en début de scolarité. Cela suppose une cohérence d’équipe certaine.
- osez ! Les premiers temps, premières semaines il vous arrivera sûrement d’être déstabilisé, étonné, interrogé par des stratégies, des façons de faire, des procédures inhabituelles. Puis, très vite, parce que « s’adapter » est une compétence partagée par tous les enseignants, vous saurez tirer parti d’une progression et de procédures pédagogiques spécifiques proposées par la méthode. Bonne aventure !
